1) Χαρακτηριστικά μεγέθη των αντιστάσεων
α. Τιμή αντίστασης Είναι η τιμή της αντίστασης με μονάδα μέτρησης το Ωμ.
β. Ισχύς της αντίστασης Είναι η μέγιστη τιμή της ισχύος που μπορεί να καταναλωθεί πάνω στην αντίσταση υπό μορφή θερμότητας.
γ. Ανοχή Είναι η απόκλιση της τιμής της αντίστασης από την τιμή που δίνει ο κατασκευαστής. Οι τιμές ανοχής ορίζονται από τον κατασκευαστή και είναι ±10%, ±5%, ±2%, ±1% και ±0,5%.
δ. Γραμμικότητα Οι αντιστάσεις στην λειτουργία τους πρέπει να ακολουθούν τον νόμο του Ohm ( I=V/R), για να μην παρατηρούνται μεταβολές των τάσεων και των εντάσεων στις οποίες λειτουργούν. Στις μη γραμμικές αντιστάσεις όμως επιδιώκουμε τέτοιες μεταβολές.
ε. Τάση θορύβου Η θερμότητα που αναπτύσουν οι αντιστάσεις στο σώμα τους έχουν σαν αποτέλεσμα να δημιουργείται θερμικός θόρυβος στο κύκλωμα με συνέπεια την ύπαρξη παρασιτικής τάσης στα άκρα τους που μετριέται σε μV ανά V της ονομαστικής τάσης λειτουργίας τους.
ζ. Σταθερότητα της αντίστασης Η συνεχείς λειτουργία της αντίστασης, στο πέρασμα του χρόνου παρουσιάζει αλλοιώσεις στο υλικό κατασκευής της με αποτέλεσμα την αλλοίωση της ονομαστικής τιμής της. Η σταθερότητα της αντίστασης εκφράζεται με την σταθερότητα της ονομαστικής της τιμής ανεξάρτητα του χρόνου λειτουργίας της.
2) Κώδικες αντιστάσεων
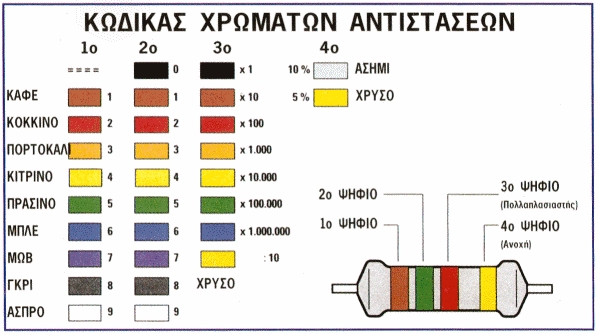
Σε σταθερές αντιστάσεις από 2 Watt και πάνω, η ονομαστική τιμή, η ισχύς και η ανοχή της αντίστασης αναγράφεται στο κέλυφός τους λόγω του μεγάλου μεγέθους της. Για σταθερές αντιστάσεις μικρής ισχύος, από 1 Watt και κάτω δηλαδή, έχει επινοηθεί ένας χρωματικός κώδικας ο οποίος εκφράζεται με δύο διαφορετικές μεθόδους. Η πρώτη μέθοδος είναι με της χρωματικές δακτυλιοειδής λωρίδες που υπάρχουν στο σήμα της αντίστασης, ενώ η δεύτερη μέθοδος είναι με διαφορετικό τρόπο υπολογισμού της τιμής, όπως θα δούμε παρακάτω.
Α. μέθοδος ανάγνωσης χρωματικού κώδικα
Η μέθοδος αυτή είναι και η ποιο δημοφιλής, καθώς όταν αγοράζουμε αντιστάσεις μικρής ισχύος θα συναντούμε πάντα αυτόν τον χρωματικό κώδικα και θα πρέπει να μπορούμε εύκολα και γρήγορα να διαβάζουμε τις τιμές των αντιστάσεων. Σύμφωνα με αυτή τη μέθοδο υπάρχουν τουλάχιστον τρεις χρωματικές δακτυλιοειδής λωρίδες πάνω στο σώμα της αντίστασης. Υπάρχουν 12 συνολικά χρώματα τα οποία χρησιμοποιούνται για να καθορίσουν την τιμή της αντίστασης, όπως βλέπουμε και στον πίνακα χρωμάτων. Στο σώμα της αντίστασης συνήθως παρατηρούμε τουλάχιστον 4 χρωματικές λωρίδες, όπου η μία βρίσκεται σε μεγαλύτερη απόσταση από τις υπόλοιπες και καθορίζει την ανοχή της αντίστασης. Κρατάμε στο χέρι μας την αντίσταση κατά τέτοιον τρόπο ώστε η λωρίδα της ανοχής της αντίστασης να βρίσκεται δεξιά μας.
Από αριστερά η πρώτη χρωματική λωρίδα δίνει το πρώτο ψηφίο του αριθμού που παριστάνει την τιμή της αντίστασης. Η δεύτερη κατά σειρά χρωματική λωρίδα μας δίνει το δεύτερο ψηφίο του αριθμού της ονομαστικής τιμής της αντίστασης, ενώ το τρίτο κατά σειρά είναι ο πολλαπλασιαστής. Ουσιαστικά το τρίτο ψηφίο μας δίνει τον αριθμό των μηδενικών μετά από τα δύο πρώτα ψηφία και συνολικά την ονομαστική τιμή της αντίστασης σε Ωμ. Το τέταρτο ψηφίο όπως αναφέραμε και πριν είναι η τιμή της ανοχής της αντίστασης και για αντιστάσεις 4 λωρίδων συνήθως έχουν χρώμα ή χρυσαφί ή ασημί, που σημαίνει ότι έχει ανοχή ή 5%, ή 10% σύμφωνα με τον παρακάτω πίνακα.
3) Μεταβλητές αντιστάσεις – ποτενσιόμετρα
Οι αντιστάσεις μεταβλητής τιμής είναι εκείνες που μπορούμε να μεταβάλουμε την ονομαστική τους τιμή και κατασκευάζονται από άνθρακα ή σύρμα ανάλογα με την ισχύ τους. Το ποτενσιόμετρα ή τα τρίμμερ που χρησιμοποιούμε, είναι μεταβλητές αντιστάσεις κυρίως από άνθρακα, ενώ για μεγαλύτερες ισχύς κατ6ασκευάζονται από αγωγό υψηλής αντίστασης. Στην κατασκευή τους συνήθως αποτελούνται από μια μονωτική πλάκα πάνω στην οποία στηρίζεται το υλικό της αντίστασης και ένας δρομέας περιστρεφόμενος εφάπτεται πάνω στο υλικό και έτσι κατασκευάζονται τα τρίμμερ και τα ποτενσιόμετρα χαμηλής ισχύος. Οι μεταβλητές αντιστάσεις σύρματος στην κατασκευή τους αποτελούνται από ένα μονωτικό υλικό κυλινδρικής μορφής, πάνω στο οποίο τυλίγεται ένας αγωγός υψηλής αντίστασης. Πάνω στον συρμάτινο αγωγό εφάπτεται ένας δρομέας ο οποίος ολισθαίνει κατά μήκος της αντίστασης σύρματος με αποτέλεσμα να παίρνουμε την μεταβλητή τιμή της αντίστασης που θέλουμε.
Τα ποτενσιόμετρα άνθρακα χωρίζονται σε δύο κατηγορίες: α) στα γραμμικά ποτενσιόμετρα και β) στα λογαριθμικά ποτενσιόμετρα. Τα γραμμικά ποτενσιόμετρα είναι εκείνα που η τιμή της αντίστασης μεταβάλλεται με σταθερό βήμα ανάλογα με την γωνία στροφής του ποτενσιομέτρου.
Τα λογαριθμικά ποτενσιόμετρα ή αλλιώς μη γραμμικά, είναι εκείνα που η αντίστασή τους μεταβάλλεται στην αρχή αργά και κατόπιν γρηγορότερα και η παραμικρή αύξηση της γωνίας στροφής του δρομέα προκαλεί απότομη μεταβολή της αύξησης ή μείωσης της τιμής της αντίστασης με μεγάλη διαφορά τιμής από την προηγούμενη θέση.
Τα λογαριθμικά ποτενσιόμετρα χρησιμοποιούνται για την ρύθμιση της έντασης ήχου (volume control), σε ενισχυτές και προενισχυτές ήχου ενώ τα γραμμικά σε κυκλώματα τα οποία θέλουμε να έχουμε σταθερό βήμα και ακρίβεια στην ρύθμιση.
Τα ποτενσιόμετρα αναγράφουν την ονομαστική τους τιμή, καθώς και τον τύπο τους, δηλαδή αν είναι γραμμικά ή λογαριθμικά. Τα γραμμικά ποτενσιόμετρα αναγνωρίζονται από το γράμμα Α, ενώ τα λογαριθμικά από το γράμμα Β.
4) Συνδεσμολογίες αντιστάσεων
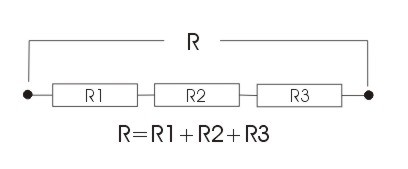
Α) Αντιστάσεις σε σειρά.
Η σύνδεση αντιστάσεων σε σειρά ορίζεται ως η σύνδεση του ενός άκρου της μιας αντίστασης με το ένα άκρο μιας δεύτερης αντίστασης, οπότε η συνολική αντίσταση θα ορίζεται από τα ελεύθερα άκρα των δύο αντιστάσεων. Στο σχήμα-1 βλέπουμε την συνδεσμολογία τριών αντιστάσεων σε σειρά. Όπως βλέπουμε και στο σχήμα, η συνολική αντίσταση R θα δίνεται από την σχέση: R=R1+R2+R3.
Αν είχαμε περισσότερες αντιστάσεις η συνολική αντίσταση θα δινόταν από την σχέση: R=R1+R2+R3+…+Rn, όπου n ο αριθμός των αντιστάσεων που ορίζει η συνδε-σμολογία.
Β) Αντιστάσεις σε παράλληλη συνδεσμολογία
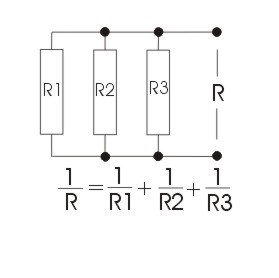
Όταν δύο ή περισσότερες αντιστάσεις έχουν ενωμένα τα άκρα τους έχουμε παράλληλη συνδεσμολογία. Στο σχήμα-2 βλέπουμε την παράλληλη συνδεσμολογία τριών αντιστάσεων. Όταν συνδέουμε παράλληλα αντιστάσεις έχουμε μείωση της συνολικής αντίστασης. Στο διπλανό σχήμα με τρεις παράλληλες αντιστάσεις η συνολική αντίσταση R θα δίνεται από την σχέση: 1/R=1/R1 + 1/R2 + 1/R3.
Αν είχαμε περισσότερες αντιστάσεις η συνολική αντίσταση R θα δίνονταν από την σχέση: 1/R=1/R1 + 1/2 + 1/R3 +…+ 1/Rn, όπου n ο αριθμός των αντιστάσεων που συνδέονται παράλληλα.